NormalMap

inline void ExtractTBN(in half3 normalOS, in float4 tangent, inout half3 T, inout half3  B, inout half3 N)
{
    N = TransformObjectToWorldNormal(normalOS);
    T = TransformObjectToWorldDir(tangent.xyz);
    B = cross(N, T) * tangent.w * unity_WorldTransformParams.w;
}

inline half3 CombineTBN(in half3 tangentNormal, in half3 T, in half3  B, in half3 N)
{
    return mul(tangentNormal, float3x3(normalize(T), normalize(B), normalize(N)));
}

Varyings vert(Attributes IN)
{
    ExtractTBN(IN.normalOS, IN.tangent, OUT.T, OUT.B, OUT.N);
}

half4 frag(Varyings IN) : SV_Target
{
    half3 normalTex = UnpackNormal(SAMPLE_TEXTURE2D(_NormalTex, sampler_NormalTex, IN.uv));
    half3 N = CombineTBN(normalTex, IN.T, IN.B, IN.N);
}
  • NormalMap(법선맵)을 쓰는 이유?
  • TBN이란?
  • world-Normal 구하는 법?
  • 노말맵 혹은 법선맵(tangent space)에서 g채널을 뒤집는 이유?

법선맵을 쓰는 이유

  • 정점(vertex)을 많이 밖아서 디테일을 표시하면, 실시간으로 정점을 처리하는데 부하가 걸린다(주로 CPU).
  • 셰이더 계산시 법선맵에서 가상의 정점을 생성해 빛을 계산하면 디테일을 살릴 수 있다.

Object Space vs Tangent Space

  • 리깅을 사용하는 모델의 경우 정점이 몰핑되면서 노말 벡터의 방향이 바뀌게 되는데 이때는 고정된 오브젝트 의 공간좌표계는 의미가 없어짐.

TBN

TBNSourcexyzUV
TangentTANGENTxu
Binormalcross(T, N)yv
NormalNORMALz
N = mul(mat_I_M, normalOS);
T = mul(tangentOS, mat_M);
B = mul(binormalOS, mat_M);
// unity같이 binormalOS를 못어올 경우 N, T를 이용하여 B를 만들 수 있다.
// B = cross(N, T) * tangentOS.w

======== 월드공간 T / B / N 을 구하고 TBN매트릭스(tangent -> world)를 만든다
float3x3 TBN_Tangent2World = float3x3(normalize(Input.T), normalize(Input.B), normalize(Input.N));
| Tx Ty Tz |
| Bx By Bn |
| Nx Ny Nz |

mul(tangentNormal, TBN_Tangent2World);   // 왠지 이케 해버리면 앞서 말한 NormalScaleProblem에 걸릴것 같음


======== TBN은 직교행렬, 직교행렬의 역행렬은 전치행렬.
TBN_World2Tangent = transpose(TBN_Tangent2World);
| Tx Bx Nx |
| Ty By Ny |
| Yz Bz Nz |

mul(TBN_World2Tangent, tangentNormal);   // 이케하면 되겠지?

======== 뇌피셜
// 위에꺼도 맞긴 맞는데...
// TBN은 직교행렬, 직교행렬의 역행렬은 전치행렬.
// traspose(inverse(M)) == M
mul(tangentNormal, TBN_Tangent2World);  // 따라서 이케해도 문제될꺼 없음? 확인해봐야함

normal flatten


//                               T, B, N
const float3 vec_TBN_UP = float3(0, 0, 1);

normalTS = lerp(normalTS, vec_TBN_UP, _Flatteness);

Block Compression
DXT5BC3 format(x, y, 0, 1)
DXT5nmDXT5의 R채널값이 A채널로 이동된것(1, y, 0, x)
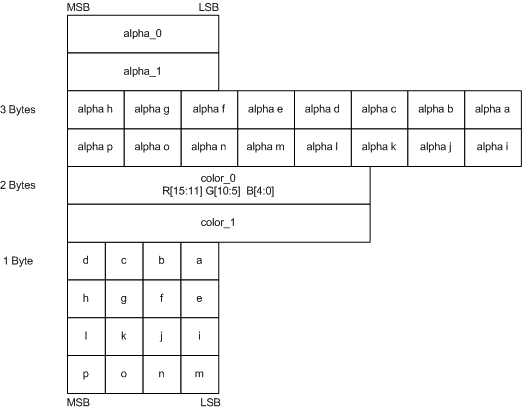
BC3channelbit
xa0, a116
alpha indices48
ycolor0,132
color indices32

d3d10-compression-bc3.png

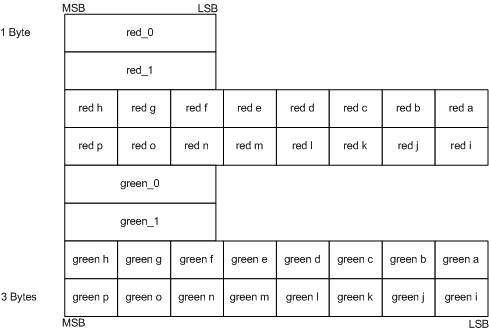
BC5channelbit
xr0, r116
red indices48
yg0, g132
green indices32

d3d10-compression-bc5.png

UNITY_NO_DXT5nm

DXT5nm이 아닌 경우(UNITY_NO_DXT5nm) 는 다음과 같은 공식을 썼으나,

real3 UnpackNormalRGBNoScale(real4 packedNormal)
{
    return packedNormal.rgb * 2.0 - 1.0;
}

아닌경우 UnpackNormalmapRGorAG을 사용 DXT5, DXT5nm을 처리할 수 있게한다.

real3 UnpackNormal(real4 packedNormal)
{
#if defined(UNITY_ASTC_NORMALMAP_ENCODING)
    return UnpackNormalAG(packedNormal, 1.0);
#elif defined(UNITY_NO_DXT5nm)
    return UnpackNormalRGBNoScale(packedNormal);
#else
    // Compiler will optimize the scale away
    return UnpackNormalmapRGorAG(packedNormal, 1.0);
#endif
}

// Unpack normal as DXT5nm (1, y, 0, x) or BC5 (x, y, 0, 1)
real3 UnpackNormalmapRGorAG(real4 packedNormal, real scale = 1.0)
{
    // Convert to (?, y, 0, x)
    packedNormal.a *= packedNormal.r;
    return UnpackNormalAG(packedNormal, scale);
}

real3 UnpackNormalAG(real4 packedNormal, real scale = 1.0)
{
    real3 normal;
    normal.xy = packedNormal.ag * 2.0 - 1.0;
    normal.z = max(1.0e-16, sqrt(1.0 - saturate(dot(normal.xy, normal.xy))));

    // must scale after reconstruction of normal.z which also
    // mirrors UnpackNormalRGB(). This does imply normal is not returned
    // as a unit length vector but doesn't need it since it will get normalized after TBN transformation.
    // If we ever need to blend contributions with built-in shaders for URP
    // then we should consider using UnpackDerivativeNormalAG() instead like
    // HDRP does since derivatives do not use renormalization and unlike tangent space
    // normals allow you to blend, accumulate and scale contributions correctly.
    normal.xy *= scale;
    return normal;
}
  • xyzw, wy => _g_r => rg => xyn // r이 뒤로 있으므로, 한바퀴 돌려줘야함.
  • normal.xy = packednormal.wy * 2 - 1; (0 ~ 1 => -1 ~ 1)
  • Z는 쉐이더에서 계산. 단위 벡터의 크기는 1인것을 이용.(sqrt(x^2 + y^2 + z^2) = 1) sqrt(1 - saturate(dot(normal.xy, normal.xy)))

Normal Scale Problem

오브젝트를 스케일시킬때 Normal의 변화의 문제

A라는 도형을 x에 대해서 2만큼 스케일 업하고 싶다고 가정하면,

정점x 스케일노말
A(1, 1)1(1, 1)
B(2, 1)2(2, 1)
C(2, 1)2(0.5, 1)

res

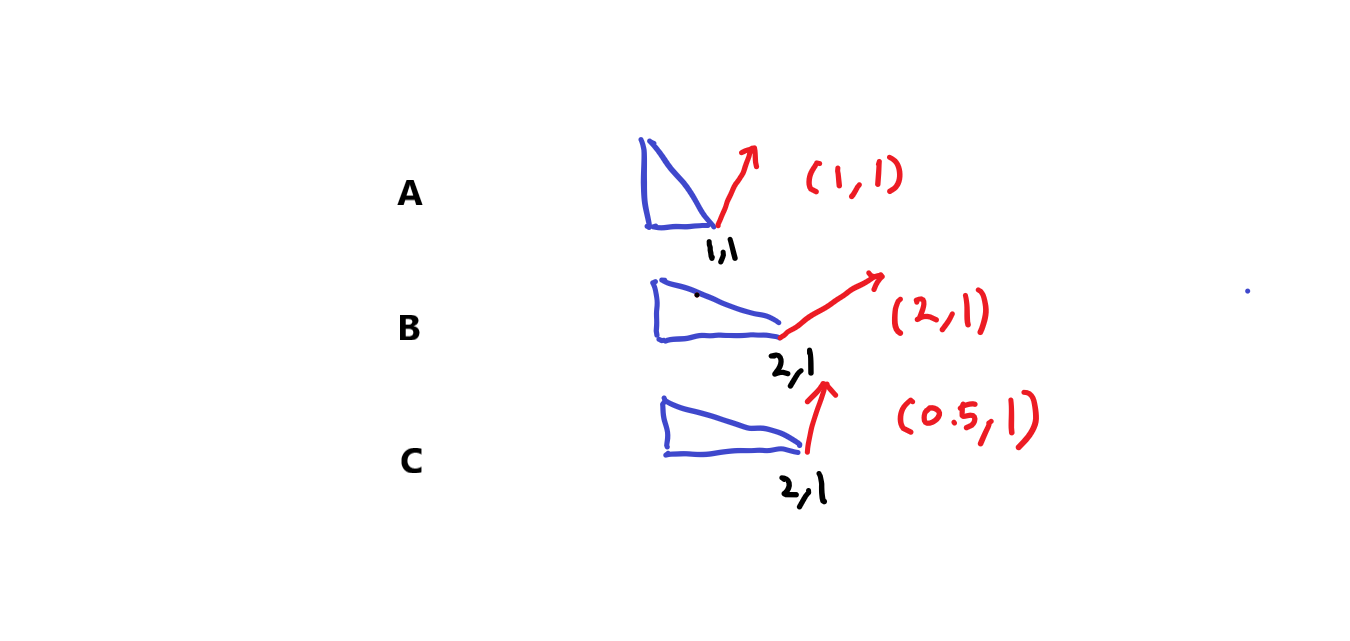
C처럼 x의 스케일 2배 됐다고, 노멀의 x값에 곱하기 2를 해서는 안된다. 역인 나누기 2 를 해야한다.

위치(position)에 대해서는 world-Position = mul(obj-Position, M )이 정상적으로 성립되었다.

하지만, world-Normal = mul( obj-Normal, M ) 처럼 적용했을시 앞+선 B와 같은 문제가 발생한다.

월드행렬(M)식으로 나타내면

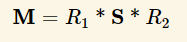
normal-1

우리가 구하고 싶은 행렬을 M-want라 했을시 world-Normal = mul(M-want, obj-Normal)

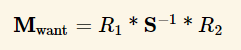
normal-2

1 2 3

즉 M-want = traspose(inverse(M)).

DirectX기준 row-major에서의 메트릭스와 벡터의 인자 순서: mul(벡터, 메트릭스) = mul( transpose(메트릭스), 벡터 )

아레 예는 row-major 기준으로 작성.

M          = ObjectToWorld
inverse(M) = WorldToObject
M-want     = traspose(inverse(M))

world-Normal
= mul(obj-Normal   , M-want              )
= mul(obj-Normal   , traspose(inverse(M)))
= mul(inverse(M)   , obj-Normal          )
= mul(WorldToObject, obj-Normal          )

노말맵 혹은 법선맵(tangent space)에서 g채널을 뒤집는 이유

노말맵에서 z값이 강한 경우가 있는데 그럼 이미지가 퍼렇게 보이면서 돌출이 아닌 움푹 패인듯한 느낌이 든다.

  • 표면 안쪽으로 향하는(z의 값이 음수인) 경우가 없다.
    • 범위는 0 ~ 1
    • 바이너리 저장시 범위가 0.5 ~ 1로 변경되면서 0.5부터 값이 시작된다.
  • 따라서 맵이 퍼렇게 보이면서, 돌출되는 부분이 이미지상 움푹들어간 모습처럼 보인다.

그러므로, g채널을 뒤집어주면 돌출된 부분을 아티스트가 쉽게 인지할 수 있다.

OpenGLY+ / DirectX Y-

../res/directx_opengl_normalmap.png

  • 유니티는 OpenGL(Y+) 를 써서 보기 비교적 편하다.
  • DirectX와 같은 엔진에서는 작업자를 위해 Y+텍스쳐 제작 쉐이더에서 y에 -1을 곱해 뒤집어 주는 코드를 넣어주면 작업자들이 편해진다.

MikkTSpace

URP셰이더 그래프URP Lit
8.1.0픽셀당 MikkTSpace 노멀 맵정점당
8.2.0픽셀당픽셀당
  • 노말맵 베이크
    • 방식1. 하이트맵이나 일반 이미지를 이용해서 노멀맵 변환
    • 방식2. 로우폴리곤과 하이폴리곤을 가지고 베이크
      • 3D프로그램 별 에버레지 버텍스 노말에 동일한 연산을 하지 않음.
        • 동일한 연산을 하도록 MikkTSpace로 통일.

Ref