넷평 남짓한 공간

egonSchiele
- blog
- twitter
- Haskell, Ruby에 관심이 많으며, 그림에도 소질이 있어 보인다.
original site link

이 글을 읽기 전에 우선 functor가 무엇인지 알아야 됩니다. functor에 대해 배우고 싶으시다면 이 글을 읽으시길 바랍니다.

자, 이제 여러분이 게임을 만든다고 가정해봅시다:

data Point = Point { _x, _y   :: Double }
data Mario = Mario { _location :: Point }

player1 = Mario (Point 0 0)

그럼, 이제 어떻게 플레이어를 움직일까요?

moveX (Mario (Point xpos ypos)) val = Mario (Point (xpos + val) ypos)

lenses로 대신, 다음과 같이 작성할 수 있습니다:

location.x `over` (+10) $ player1

아니면, 다음과 같이 말이죠:

over (location . x) (+10) player1

Lenses를 이용하여 data의 일 부분을 선택적으로 변경할 수 있습니다:

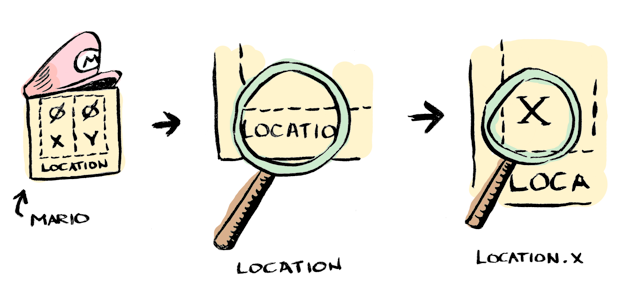
훨씬 깔끔합니다! 전체 예제는 여기에 있습니다.

location은 lens입니다. 그리고 x도 lens입니다. 여기선 player의 일부분을 수정하기 위해 이러한 lens들을 조합하였습니다.

Fmap

fmap이 어떻게 동작하는지 자네는 아마 잘 알거야, Doctor Watson. (잘 모르시겠다면 이 글을 읽으시길 바랍니다.)

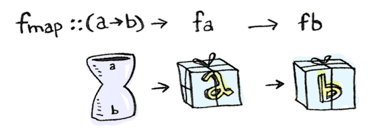
이전 장에서, 과연 functor가 중첩되어 있다면 어떨까요?

fmap을 두번 사용해야만 할껍니다!

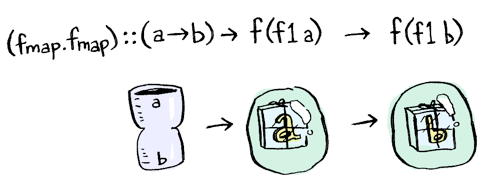
지금, 아마 여러분은 function composition이 어떻게 동작하는지 알고 있을 것입니다:

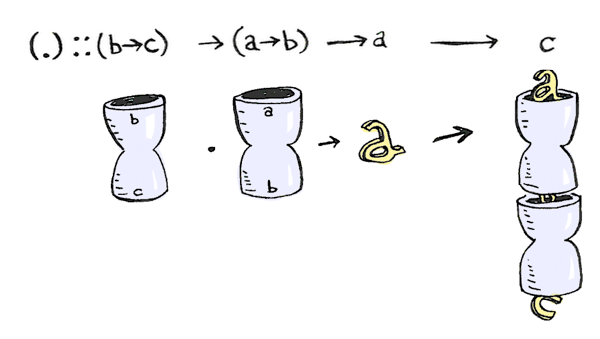
그렇다면, function composition의 composition은 어떨까요?

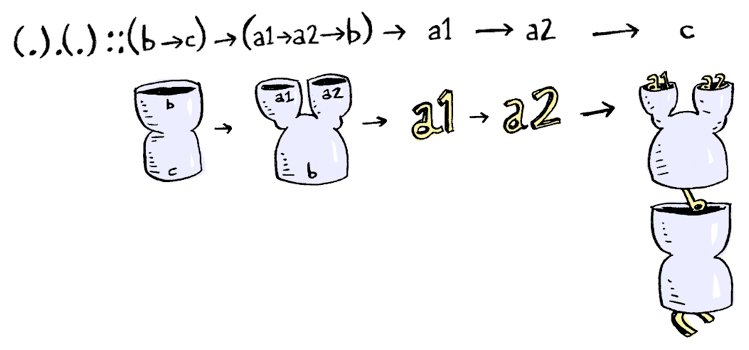
"두개의 인자를 가진 함수에 function composition을 적용하고자 한다면", Sherlock이 말하길, "(.).(.)가 필요할걸세!"

"마치 부엉이가 놀란것처럼 보여", Watson은 외쳤습니다.

"정말 그렇군. 그럼 왜 이게 동작하는지 살펴보자고"

function composition의 type signature는:

(.) :: (b -> c) -> (a -> b) -> (a -> c)

fmap과 무척 닮아 있습니다!

fmap :: (a -> b) -> f a -> f b

사실, a ->를 f로 바꾸면 그게 바로 fmap입니다!

a ->가 functor라면 다음과 같이 정의할 수 있을 것입니다:

instance Functor ((->) r) where
   fmap = (.)

함수에게 있어, fmap은 단지 function composition입니다! (.).(.)은 fmap . fmap와 동일합니다!

(.).(.) :: (b -> c) -> (a1 -> a2 -> b) -> (a1 -> a2 -> c)
fmap . fmap :: (a -> b) -> f (f1 a) -> f (f1 b)

저희는 여기서 패턴을 발견할 수 있습니다: fmap . fmap과 (.) . (.)은 "한 단계 깊이" 들어갈 수 있도록 해준다. fmap에서 이는 functor 안으로 들어갈 수 있다는 것을 의미합니다. function composition에서 함수는 r ->이며, 이는 함수에 하나의 인자를 더 넘길 수 있다는 것을 의미합니다.

Setters

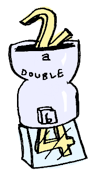
다음과 같이 double이란 함수가 있다고 가정해봅시다:

double :: Int -> Maybe Int
double x = Just (x * 2)

traverse로 list에 이 함수를 적용할 수 있습니다.

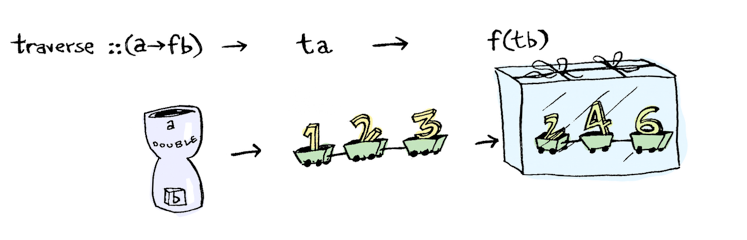
traverse가 가능한 것과, functor로 감싸진 값을 반환하는 함수를 넘기면, traverse가 가능하지만 functor로 감싸진 것을 돌려받게됩니다.

평소처럼, traverse을 조합하여, 한단계 더 나아가 보도록 하겠습니다.

traverse :: (a -> m b) -> f a -> m (f b)
traverse.traverse :: (a -> m b) -> f (g a) -> m (f (g b))

fmap을 traverse로 정의할 수 있어, 보다 강력해보입니다:

fmapDefault :: Traversable t => (a -> b) -> t a -> t b
fmapDefault f = runIdentity . traverse (Identity . f)

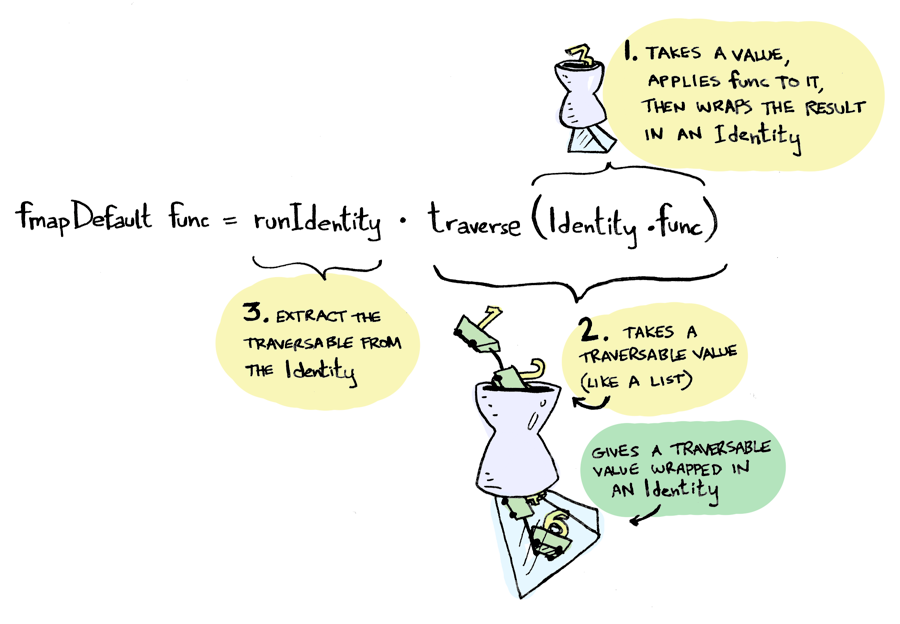
Identity는 언제 쓰일까요? 답을 확인해 봅시다.

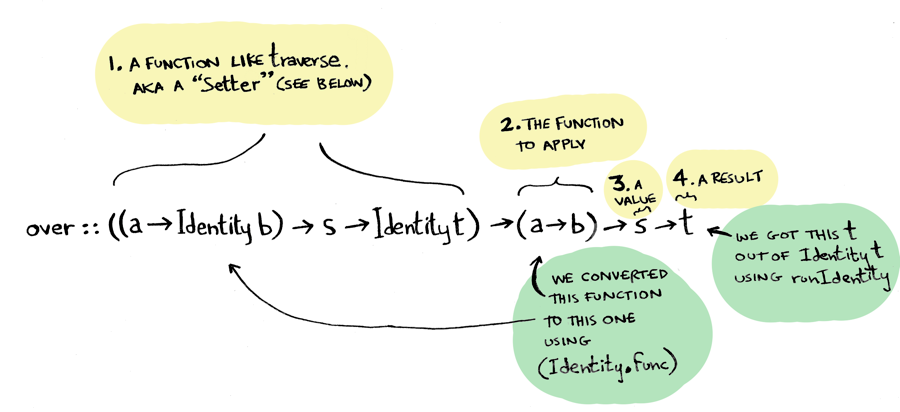
fmapDefault을 이용하여, over라는 함수를 만들어 보도록 하겠습니다. over에 traverse을 넘기지 않았다는 점을 뺀다면 fmapDefault와 같습니다:

over :: ((a -> Identity b) -> s -> Identity t) -> (a -> b) -> s -> t
over l f = runIdentity . l (Identity . f)

-- over traverse f == fmapDefault f

이제 저희는 lenses에 매우 가까이 다가왔습니다! "음 Watson, 나는 lenses를 맛볼(taste) 수 있어. Sherlock이 침을 흘리며 말했습니다. "Lenses는 functor, fold, traversal들을 함께 compose할 수 있게 만들어주지. 지금, 내 입에서 functor와 fold가 합쳐진것을 느낄 수 있어!"

여기서 빨리 type alias를 만들어야겠습니다:

type Setter s t a b = (a -> Identity b) -> s -> Identity t

이제 저희는 over를 더욱 깔끔하게 작성할 수 있게 되었습니다:

over :: Setter s t a b -> (a -> b) -> s -> t

-- same as:
over :: ((a -> Identity b) -> s -> Identity t) -> (a -> b) -> s -> t

over는 Setter취하고
transform 함수와
위 함수에 적용시킬 값도 취한 다음
setter를 이용하여, 받은 함수로 받은 값의 일부를 변경한다.

mario를 기억하십니까? 이제 다음 라인이 더 잘 이해가 될겁니다:

location.x `over` (+10) $ player1

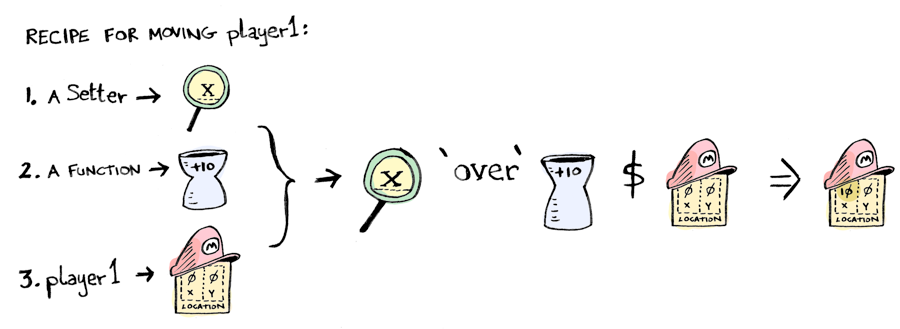
location . x는 setter입니다. 그리고, location과 x 역시 setter입니다! fmap나 (.)를 composing 한것처럼 한 단계 더" 나아갈 수 있게 만들어주며, setter들을 compose하여 data 내부에 좀 더 깊이 내려갈 수 있습니다! 멋지지 않을 수 없습니다!

Folds

lenses를 만드는 것에 한단계 더 나아가게 되었습니다. functor를 compose할 수 있는 setter를 만들었습니다.

사실, fold로도 동일한 일을 할 수 있습니다. 먼저, foldMapDefault를 정의해 보겠습니다:

foldMapDefault :: (Traversable t, Monoid m) => (a -> m) -> t a -> m
foldMapDefault f = getConst . traverse (Const . f)

Const가 하는 일은?

위에서 정의한 fmapDefault과 모양이 매우 비슷합니다! 결국에는 Fold라는 새로운 type alias얻어낼 수 있습니다:

type Fold s t a b = forall m. Monoid m => (a -> Const m b) -> s -> Const m t

Setter와 무척 닮았습니다:

type Setter s t a b = (a -> Identity b) -> s -> Identity t

Fold의 전체 어원

Fold와 Setter의 signature가 무척 닮아있기에, 하나의 type alias로 묶을 수 있습니다. 그리고 저희는 할 수 있습니다!

type Lens s t a b = forall f. Functor f => (a -> f b) -> s -> f t

Lenses

Setters는 functor를 위한 것이며 Folds는 fold를 위한 것이지만, lenses는 더욱 general한 타입입니다. 이는 functor, function, fold, traversal을 함께 뭉칠 수 있게 만들어 줍니다! 여기 예제 하나가 있습니다:

tuple에 fmap을 했을때, 두번째에만 효과가 있는 것이 짜증나지 않으셨습니까?

> fmap (+10) (1, 2)
(1,12)

둘 다에 적용시키려면 어떻게 할까요? lens를 작성하면 됩니다!

> both f (a,b) = (,) <$> f a <*> f b

그런 다음, 이를 이용하면:

> both `over` (+10) $ (1, 2)
(11,12)

lenses를 합쳐 더 깊이 내려 갈 수 도 있습니다! 여기 both 부분과 both부분에 함수를 적용해 보도록 하겠습니다:

> (both . both) `over` (+2) $ ((1, 2), (3, 4))
((3,4),(5,6))

또한, setter와 fold에 대해서도 합칠 수 있습니다!

결론

data가 많이 중첩되어 있다면, lenses는 매우 유용하게 쓰일 수 있습니다. 그리고 이들의 어원 역시, 매우 멋있는 부분입니다! 전체 어원

lenses를 마구 삼키는 Sherlock

이러한 시각적 접근이 맘에 든다면, concurrency에 대해 쓴 제 글을 살펴봐 주시기 바랍니다.

Lenses In Pictures

Fmap

Setters

Folds

Lenses

결론

참고자료