egonSchiele
- blog
- twitter
- Haskell, Ruby에 관심이 많으며, 그림에도 소질이 있어 보인다.
original site link

여기, 단순한 값(value)이 있습니다.

Prelude> 2
2

그리고, 우리는 이 값에 함수(function)를 적용하는(apply) 법을 알고 있습니다.

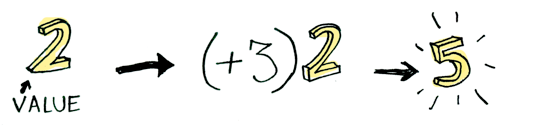
Prelude> (+3) 2
5

아주 간단합니다. 그럼 이제, 이 값이 어떠한 상태(context)안에 들어있다고 가정해봅시다. 이제 여러분은 값을 담을 수 있는 어떠한 상태를, 상자라고 생각할 수 있을 것입니다.

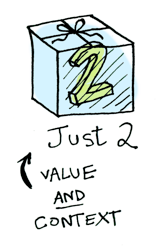
Prelude> Just 2
Just 2

이제, 이 값에 함수를 적용하게 되면, 상태에 따라 다른 결과를 얻게 될 것입니다.

Functors, 이를 기반으로한 개념(idea) 중에는 Applicatives, Monads, Arrows 등이 있습니다. Maybe 데이터 타입은 두가지 상태로 정의할 수 있습니다.

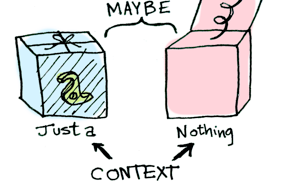
data Maybe a = Nothing | Just a

Prelude> :type Just
Just :: a -> Maybe a

Prelude> :type Nothing
Nothing :: Maybe a

다음으로, Just a와 Nothing의 상태에 따라, 함수가 어떻게 적용되는지 보도록 하겠습니다. 우선, Functors에 대해 이야기해 보도록 하겠습니다.

Functors

상자안에 있는 값에는, 단순한 함수를 적용할 수 없습니다.

Prelude> (+3) (Just 2)
 ERR - No instance for (Num (Maybe a0))

길거리 출신인 fmap은 상자에 대해서는 빠삭합니다. fmap은 상자안에 있는 값에 함수를 어떻게 적용해야 할지를 알고 있습니다. 예를 들어, Just 2에 (+3)를 적용시켜 봅시다. fmap을 사용해보면,

> fmap (+3) (Just 2)
Just 5

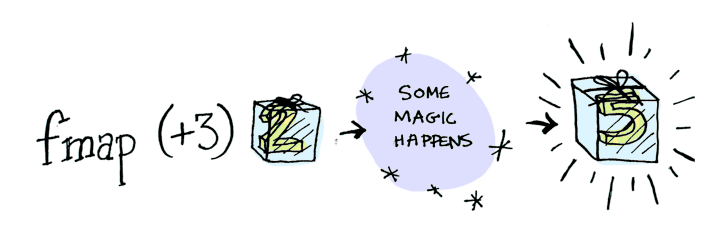
쨘! fmap이 멋지게 해냈습니다. 어떻게 fmap이 함수를 적용시키는 법을 알고 있는 걸까요?

Functor가 도대체 뭡니까?

Functor는 typeclass입니다. 여기 정의가 나와있습니다.

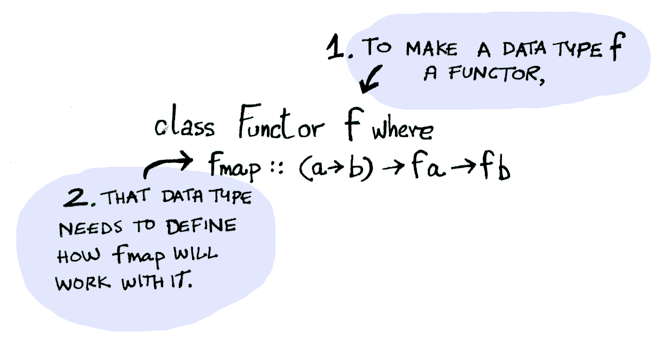
Functor는 fmap을 적용시키는 법을 정의한 데이터 타입입니다. 여기, 어떻게 fmap이 동작하는지 나와 있습니다.

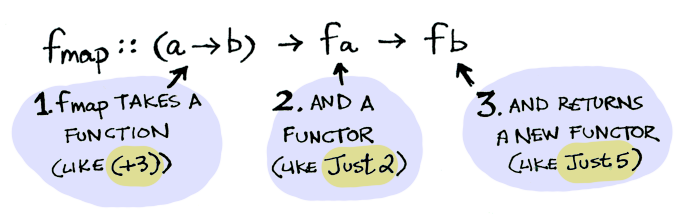
따라서, 우리는 다음과 같이 할 수 있습니다.

> fmap (+3) (Just 2)
Just 5

Maybe역시 Functor이기에, fmap은 마법과도 같이 함수를 적용하였습니다. 다음으로, Just와 Nothing에 대해 fmap을 적용시키는 방법에 대해 나와있습니다.

instance Functor Maybe where
    fmap func (Just val) = Just (func val)
    fmap func Nothing = Nothing

여기, fmap (+3) (Just 2)이라고 쳤을때, 어떠한 일이 뒤에서 일어나는지 나와있습니다.

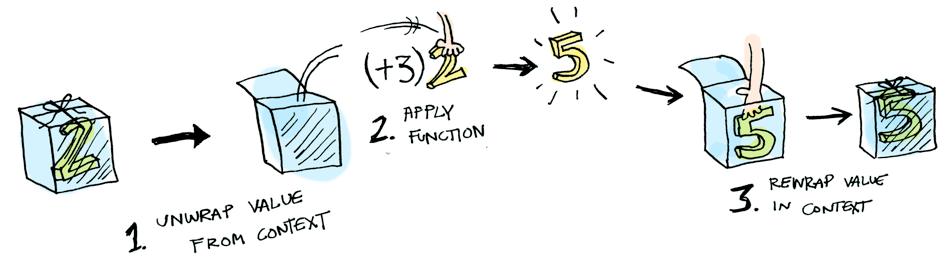
이번에는, Nothing에 (+3)을 적용시켜 보도록 하겠습니다.

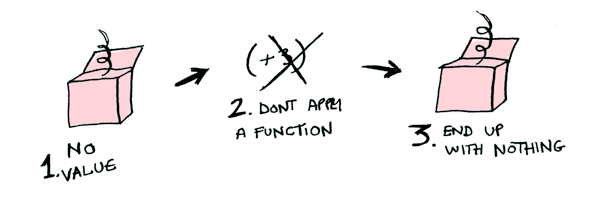
> fmap (+3) Nothing
Nothing

Maybe functor도 모르는 Bill O’Reilly

메트릭스의 모피어스처럼, fmap은 무엇을 해야할지 알고 있습니다. Nothing으로 시작하면, Nothing으로 끝난다! fmap은 zen(시작이자 끝)입니다. 이제, Maybe 데이터 타입이 왜 존재하는지 알아봅시다. 예를들어, 다음과 같이 Maybe가 없는 언어에서 데이터를 가지고 작업을 한다고 한다면,

post = Post.find_by_id(1)
if post
  return post.title
else
  return nil
end

Haskell은 다음과 같이 할 수 있습니다.

fmap (getPostTitle) (findPost 1)

만약, findPost가 게시글(post)를 반환한다면, getPostTitle로 제목(title)을 얻을 것입니다. Nothing을 반환하면, Nothing을 얻을 것입니다. 매우 간단하지 않습니까? fmap의 중위표기(infix) 버전은 <$>이며, 다음과 같이 쓰기도 합니다.

getPostTitle <$> (findPost 1)

여기, 또 다른 예가 나와있습니다. 리스트에 함수를 적용시키면 무슨일이 생길까요?

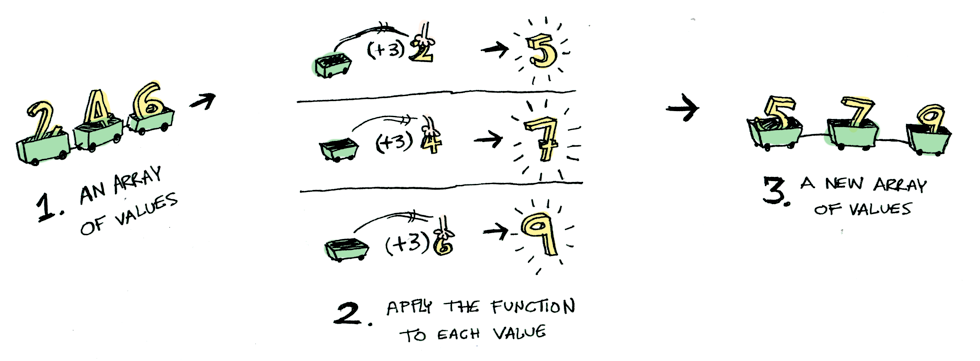
리스트 역시 Functor였던 것이였습니다! 여기 정의가 나와있습니다.

instance Functor [] where
    fmap = map

자, 자, 마지막으로 하나 더. 함수에 또 다른 함수를 적용시키면 어떤일이 벌어질까요?

fmap (+3) (+1)

Prelude> :type fmap (+3) (+1)
fmap (+3) (+1) :: (Functor ((->) b), Num b) => b -> b

여기 하나의 함수가 있습니다.

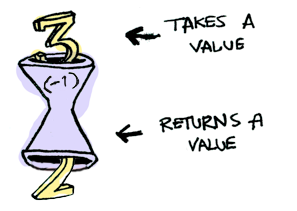
함수에 또 다른 함수를 적용해 보도록 하겠습니다.

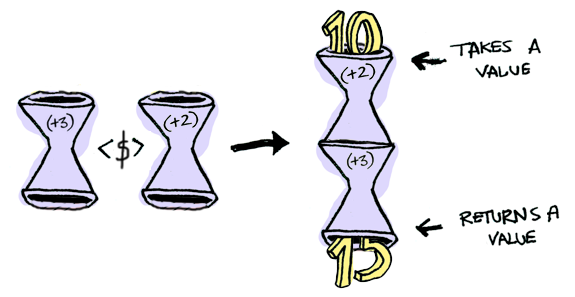
결과 역시 함수 입니다.

> import Control.Applicative
> let foo = fmap (+3) (+2)
> foo 10
15

따라서, 함수 역시 Functor입니다.

instance Functor ((->) r) where
    fmap f g = f . g

함수에 fmap을 사용하면, function composition을 한것과 같습니다.

Applicatives

다음 단계로 넘어가보도록 하겠습니다. Functors에서 나왔던 것처럼, 상자에 값을 넣습니다.

함수 역시 상자에 들어갈 수 있습니다.

그럼 자세히 살펴보도록 하겠습니다. Applicatives는 바보가 아닙니다. Control.Applicative는 상자 속 값에, 상자 속 함수를 적용하는 법을 알도록 <*>를 정의했습니다.

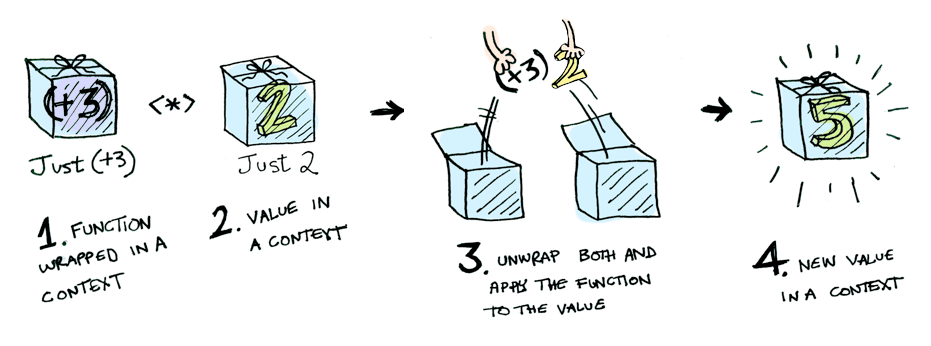
즉, 다음과 같이 할 수 있습니다.

Just (+3) <*> Just 2 == Just 5

<*>를 사용하면 조금 흥미로운 결과를 얻을 수 있습니다. 예를들면,

> [(*2), (+3)] <*> [1, 2, 3]
[2, 4, 6, 4, 5, 6]

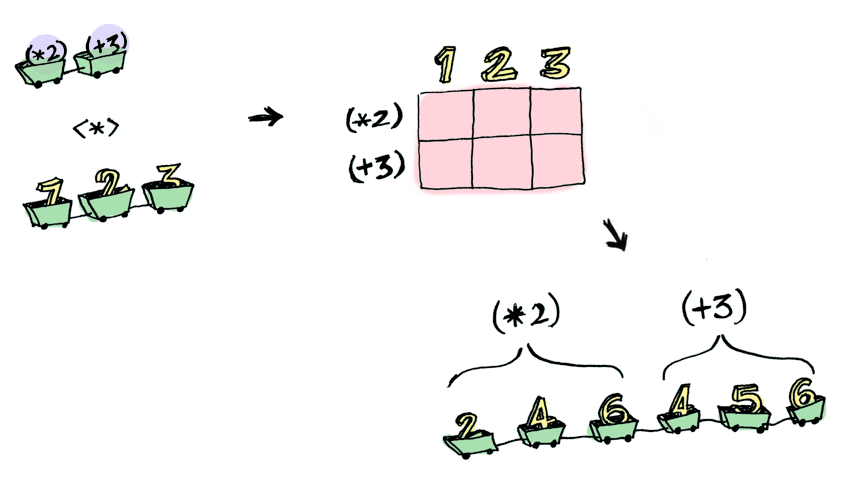
여기, Functor로는 할 수 없지만, Applicative로 할 수 있는게 나와있습니다. 두개의 인자를 취하는 함수를, 어떻게 속에 값이 들어있는 두개의 상자에 적용시킬까요?

> (+) <$> (Just 5)
Just (+5)
> Just (+5) <$> (Just 4)
ERROR ??? WHAT DOES THIS EVEN MEAN WHY IS THE FUNCTION WRAPPED IN A JUST

Applicatives:

> (+) <$> (Just 5)
Just (+5)
> Just (+5) <*> (Just 3)
Just 8

Functor을 옆으로 밀쳐내면서 Applicative이 말합니다.

"어른은 여러 인자들을 다룰 수 있는 함수를 쓰지."

"값이 들어있는 상자와 함수가 들어있는 상자를 <$>와 <*>를 이용해서, 값이 들어있는 상자를 얻을 수 있다고! ㅎㅎㅎㅎ!"

> (*) <$> Just 5 <*> Just 3
Just 15

functor가 함수를 적용시키는 것을 지켜보고 있던 applicative

잠깐! 여기 동일한 일을 하는 liftA2도 있습니다.

> liftA2 (*) (Just 5) (Just 3)
Just 15

Monads

모나드를 배우는 방법 :

컴퓨터 공학 박사학위를 딴다.
필요없으니 집어 치운다!

Monads는 새로운 해법을 제시하였습니다.

Functors는 상자에 있는 값에 함수를 적용할 수 있습니다.

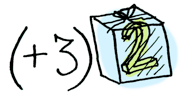
Applicatives는 상자에 있는 값에, 상자에 있는 함수를 적용 할 수 있습니다.

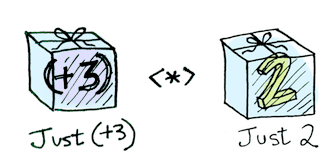
Monads는 상자에 있는 값에 함수를 적용시켜 값이 들어있는 상자를 반환 할 수 있습니다.

Monads는 이러한 일을 처리하는 ("bind"라 불리는) >>=라는 함수를 가지고 있습니다.

예제를 살표봅시다. 이제까지 봐왔던 Maybe는 모나드입니다.

놀고있던 Just a 모나드

짝수에 대해서만 동작하는 함수, half가 있다고 가정해봅시다.

half x = if even x
           then Just (x `div` 2)
           else Nothing

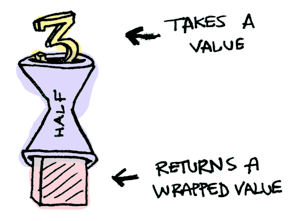
값이 들어있는 상자를 넣으면 어떻게 될까요?

함수에 값이 들어있는 상자를 밀어 넣을려면, >>=가 필요합니다. 여기, >>=의 사진이 있습니다.

어떻게 동작하는지 확인해 봅시다.

> Just 3 >>= half
Nothing
> Just 4 >>= half
Just 2
> Nothing >>= half
Nothing

내부에서 어떤일이 벌어진 걸까요? Monad는 또 다른 typeclass입니다. 여기, 정의 중 일부가 나와있습니다.

class Monad m where
    (>>=) :: m a -> (a -> m b) -> m b

>>=는,

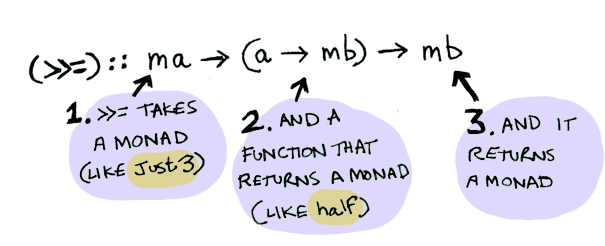
따라서, Maybe는 Monad입니다:

instance Monad Maybe where
    Nothing >>= func = Nothing
    Just val >>= func  = func val

여기, Just 3에 대 해 어떻게 동작하는지 나와있습니다!

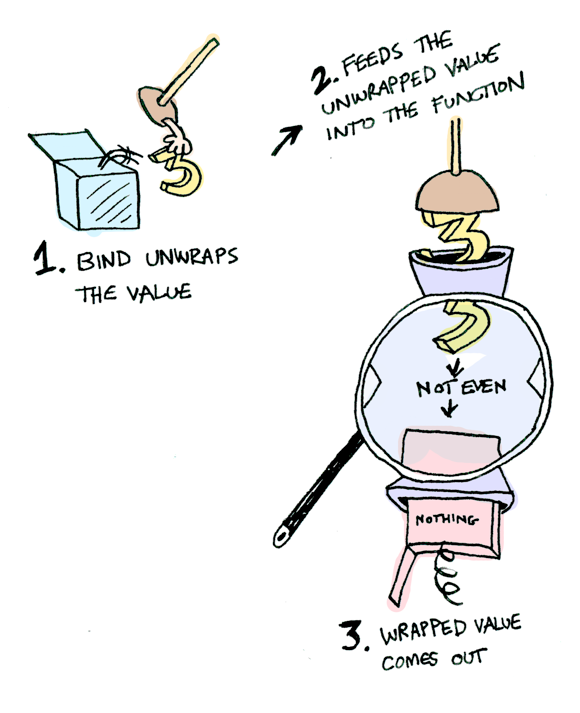
Nothing을 넣으면 보다 단순해 집니다.

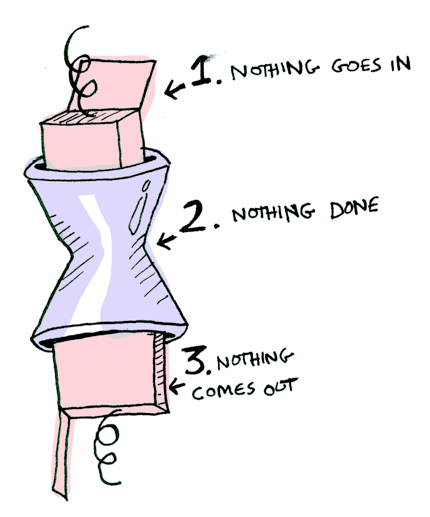
이렇게 연달아 호출할 수 도 있습니다.

> Just 20 >>= half >>= half >>= half
Nothing

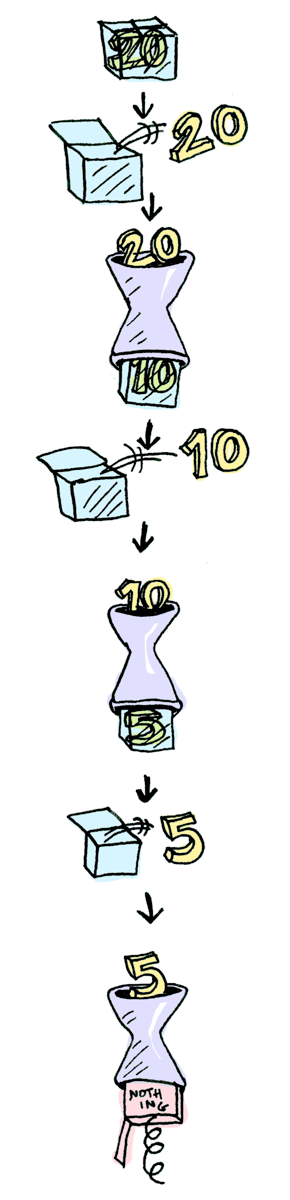
끝내줍니다. 이제 우리는 Maybe가 Functor이자, Applicative이며, Monad라는 것을 알게 되었습니다.

이제 슬슬, IO 모나드 예제로 가 보겠습니다.

숫자 10아님... 영어 IO임

세개의 특별한 함수가 있습니다. getLine은 인자를 받지 않고, 사용자의 입력을 받습니다.

getLine :: IO String

readFile는 문자열(파일명)을 받아, 파일에 있는 내용을 반환합니다.

readFile :: FilePath -> IO String

putStrLn은 문자열을 받아 출력합니다.

putStrLn :: String -> IO ()

여기 나온 세개의 함수는 평범한 값(혹은 없거나)을 받아서, 값이 들어있는 상자를 반환합니다. 따라서, 우리는 이를 >>=로 묶을 수 있습니다!

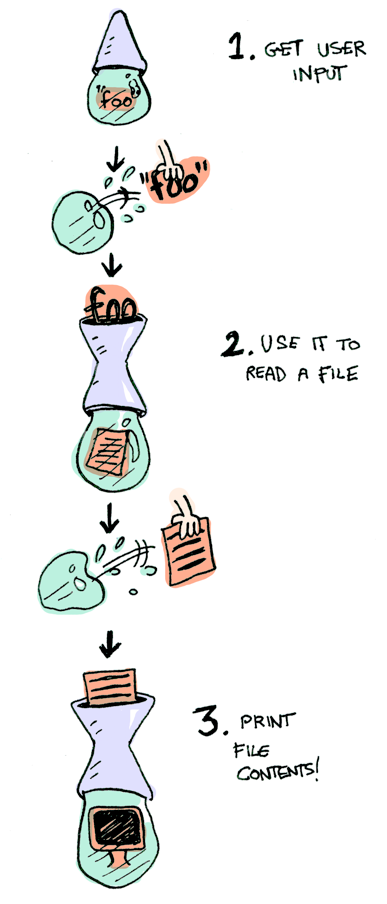
getLine >>= readFile >>= putStrLn

오 예! 모나드 쇼가 펼쳐졌습니다!

덧붙이자면, Haskell은 이 모나드에 대해, do라는 syntax suger를 제공해 주었습니다.

foo = do
    filename <- getLine
    contents <- readFile filename
    putStrLn contents

Conclusion

functor는 Functor 타입 클래스를 구현한 데이터 타입이다.
applicative는 Applicative 타입 클래스를 구현한 데이터 타입이다.
monad는 Monad 타입 클래스를 구현한 데이터 타입이다.
Maybe는 이 세개를 모두 구현했으므로, functor이자 applicative이며 monad이다.

이 셋의 차이점은 무엇일까?

functors: fmap이나 <$>를 이용하여 상자 속 값에 함수를 적용할 수 있다.
applicatives: liftA나 <*>를 이용하여 상자 속 함수를 상자 속 값에 적용할 수 있다.
monads: liftM나 >>=를 이용하여 값이 들어있는 상자를 받아 함수를 적용하고 값이 들어있는 상자를 반환할 수 있다.

우리 모두 모나드라는 것이 쉽고 멋진 개념(트레이드 마크)이라는 것에 대해, 동의한다고 생각합니다. 이 가이드로 만족하기엔 아직 이릅니다. LYAH’s section on Monads를 확인하시기 바랍니다. Miran님 께서 이미 모나드에 관한 깊고, 훌륭한 일을 해냈기에, 저는 많은 것을 얼버무리고 넘어갔습니다.

러시아 버전도 있습니다. 더 많은 모나드와 그림을 원하신다면, three useful monads를 확인하시기 바랍니다.

Functors, Applicatives, And Monads In Pictures

Functors

Functor가 도대체 뭡니까?

Applicatives

Monads

Conclusion